Gradient background images with ruby and chunky_png
- Published
- 2022-02-05
- Tagged
I recently decided that I wanted to make a series of solid colour backgrounds for my laptop. The reasons are nominally grounded in productivity1, but given that the whole exercise sent me down a rabbit-hole of writing code and then this blog post, let’s just call it a little experiment to see what we can do, shall we?
Step 1: Making a solid colour PNG
Our first step will be to create a solid colour PNG of the right size. I’m going to use the ruby gem ChunkyPNG to do all the heavy lifting. Let’s get started!
1 | #!/usr/bin/env ruby
|
2 | |
3 | require 'chunky_png' |
4 | |
5 | HEIGHT = 800 |
6 | WIDTH = 800 |
7 | |
8 | HUE = rand(360) |
9 | puts "Making a background with hue #{HUE}" |
10 | LUMINESCENCE = 0.5 |
11 | |
12 | image = ChunkyPNG::Image.new(WIDTH, HEIGHT) |
13 | |
14 | 1.upto(HEIGHT) do |y| |
15 | 1.upto(WIDTH) do |x| |
16 | image[x - 1, y - 1] = ChunkyPNG::Color.from_hsl(HUE, 1, LUMINESCENCE) |
17 | end
|
18 | end
|
19 | |
20 | image.save("background.png") |
This script:
- Sets the height and width of our image
- Picks an appropriate hue (randomly set in this instance) and luminence
- Generates the image and sets every pixel to the specified colour
- Saves it to
background.png
Here’s an example, generated using the script above:

Wow, look at all that colour
Step 2: Let’s make it prettier
OK so we can make solid colour backgrounds automatically, big deal. We can do that in MS paint! What if we want to make them look a bit cooler? And what’s cooler than an automatically generated linear gradient?
This is going to take a few steps, however, and we’re going to have to go back to high school trigonometry. Ready for some maths? Let’s get stuck in.
So: if we apply a linear gradient with an angle θ, all points situated on a line at 90° to this gradient will have the same colour. We can show this visually:
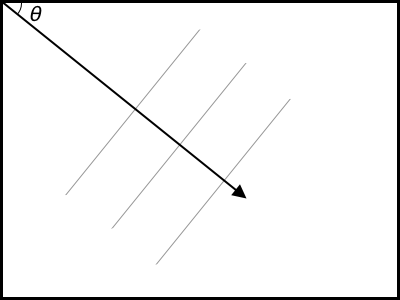
All points along the thin lines will have the same colour - they’re all at 90° to the gradient vector.
So obviously when we’re just looking at this diagram, we can trace a given point back onto that gradient line. How do we do that mathematically? We use a geometric technique called projection to see how far down the gradient line a given point falls. We can do this by imagining a given point p(x,y) as a point on a right-angled triangle, as follows:
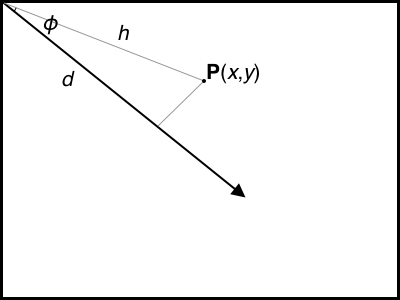
I’ll try not to introduce any more Greek letters, I swear.
OK, so what’s that distance d, the projection of the point onto the gradient? Well, we know from trigonometry that:
OK, but what does that mean? After all, right now all we know is the angle of our gradient (we get to decide this), and the x and y coordinates of our point P (we’re going to iterate over all points, so this is going to change as we go).
So how do we calculate any of these values?
Let’s start with h. This is the distance between the top-left pixel and our point P. Pythagorus has a theorem for this:
Easy! Now, what about ɸ? This is the angle of the right-angle triangle, and it’s just the difference between our gradient angle θ and, well, whatever angle our point P makes with the top of the screen. Trigonometry to the rescue:
(We mark the whole thing as absolute as we always want to have a positive value here.)
So that’s the maths. What does it look like in code? Here’s a ruby function that, given a point with a given x and y, and a given gradient, calculates the projection of the point on the gradient line:
1 | # Calculate a gradient projection, given a point (x,y) and a gradient
|
2 | # angle of `gradient` in radians.
|
3 | def gradient_projection(x, y, gradient) |
4 | |
5 | # Calculate angles
|
6 | point_angle = Math::atan(y / x) |
7 | triangle_angle = (gradient - point_angle).abs |
8 | |
9 | # Calculate distance from (0, 0) to (x, y)
|
10 | point_distance = Math::sqrt(x**2 + y**2) |
11 | |
12 | # Calculate projection
|
13 | return point_distance * Math::cos(triangle_angle) |
14 | end
|
So how do we use this in constructing a gradient? There’s all kinds of ways you can do this - in the example below I’m going to transition between two luminescence values - one at the top left and one at the bottom right:
1 | #!/usr/bin/env ruby
|
2 | |
3 | require 'chunky_png' |
4 | |
5 | # Constants
|
6 | HEIGHT = 800 |
7 | WIDTH = 800 |
8 | |
9 | # We use this for interpolating luminescence
|
10 | DIAGONAL = Math::sqrt(HEIGHT**2 + WIDTH**2) |
11 | |
12 | HUE = rand(360) |
13 | |
14 | LUMINESCENCE_START = 0.5 |
15 | LUMINESCENCE_END = 0.3 |
16 | |
17 | # We need to convert this from degrees to radians
|
18 | GRADIENT_ANGLE_DEGREES = 45 |
19 | GRADIENT_ANGLE = GRADIENT_ANGLE_DEGREES * Math::PI / 180 |
20 | |
21 | # Calculate a gradient projection, given a point (x,y) and a gradient
|
22 | # angle of `gradient` in radians.
|
23 | def gradient_projection(x, y, gradient) |
24 | |
25 | # Calculate angles
|
26 | point_angle = Math::atan(y / x) |
27 | triangle_angle = (gradient - point_angle).abs |
28 | |
29 | # Calculate distance from (0, 0) to (x, y)
|
30 | point_distance = Math::sqrt(x**2 + y**2) |
31 | |
32 | # Calculate projection
|
33 | return point_distance * Math::cos(triangle_angle) |
34 | end
|
35 | |
36 | image = ChunkyPNG::Image.new(WIDTH, HEIGHT) |
37 | |
38 | 1.upto(HEIGHT) do |y| |
39 | 1.upto(WIDTH) do |x| |
40 | |
41 | # Calculate projection as a fraction of DIAGONAL
|
42 | proj = gradient_projection(x, y, GRADIENT_ANGLE) |
43 | proj_fxn = proj / DIAGONAL |
44 | |
45 | lum = LUMINESCENCE_START + (LUMINESCENCE_END - LUMINESCENCE_START) * proj_fxn |
46 | |
47 | image[x - 1, y - 1] = ChunkyPNG::Color.from_hsl(HUE, 1, lum) |
48 | end
|
49 | end
|
50 | |
51 | image.save("background2.png") |
Looks good? It works (almost!) perfectly!

Except for one little flaw…
Astute readers will notice that something weird is going on here - the bottom-left side of the image is fine, but the top-right isn’t doing what it should. If you’re feeling like a challenge, see if you can identify the issue before reading on!
OK, if you just want to know what the issue is - it’s in how ruby treats integer division (namely, it gets rid of any fractions). This means that our issue exists in the following line:
1 | point_angle = Math::atan(y / x) |
If y < x, y / x will always equal zero. We can fix this by converting y to a floating point decimal first:
1 | point_angle = Math::atan(y.to_f / x) |

Much better.
In the end, I just stepped through all 360 degrees of hue at 10 degrees per step to create 36 backgrounds to cycle through, but you may want to pick out your favourite colours, or play around with the logic.
Bonus round: radial gradients!
We’re not just limited to linear gradients, especially not given we’re generating this pixel-by-pixel. Let’s have a go at generating a radial gradient centred on the top-left, rather than our linear gradient.
This is actually easier than the linear gradient - all we need to do is calculate the distance from top left and use that to calculate luminescence:
1 | #!/usr/bin/env ruby
|
2 | |
3 | require 'chunky_png' |
4 | |
5 | # Constants
|
6 | HEIGHT = 800 |
7 | WIDTH = 800 |
8 | |
9 | HUE = rand(360) |
10 | |
11 | LUMINESCENCE_START = 0.5 |
12 | LUMINESCENCE_END = 0.3 |
13 | |
14 | def dist(x, y) |
15 | Math::sqrt(x**2 + y**2) |
16 | end
|
17 | |
18 | DIAGONAL = dist(WIDTH, HEIGHT) |
19 | |
20 | image = ChunkyPNG::Image.new(WIDTH, HEIGHT) |
21 | |
22 | 1.upto(HEIGHT) do |y| |
23 | 1.upto(WIDTH) do |x| |
24 | |
25 | # Calculate projection as a fraction of DIAGONAL
|
26 | dist_fxn = dist(x, y).to_f / DIAGONAL |
27 | |
28 | lum = LUMINESCENCE_START + (LUMINESCENCE_END - LUMINESCENCE_START) * dist_fxn |
29 | |
30 | image[x - 1, y - 1] = ChunkyPNG::Color.from_hsl(HUE, 1, lum) |
31 | end
|
32 | end
|
33 | |
34 | image.save("background4.png") |

Easy peasy.
In fact, it’s so easy that we could even specify an origin point which isn’t the top left…
1 | #!/usr/bin/env ruby
|
2 | |
3 | require 'chunky_png' |
4 | |
5 | # Constants
|
6 | HEIGHT = 800 |
7 | WIDTH = 800 |
8 | |
9 | HUE = rand(360) |
10 | |
11 | LUMINESCENCE_START = 0.5 |
12 | LUMINESCENCE_END = 0 |
13 | |
14 | ORIGIN_X = 400 |
15 | ORIGIN_Y = 200 |
16 | |
17 | def dist(x, y) |
18 | Math::sqrt(x**2 + y**2) |
19 | end
|
20 | |
21 | def dist_from_origin(x, y) |
22 | dist(x - ORIGIN_X, y - ORIGIN_Y) |
23 | end
|
24 | |
25 | DIAGONAL = dist(WIDTH, HEIGHT) |
26 | |
27 | image = ChunkyPNG::Image.new(WIDTH, HEIGHT) |
28 | |
29 | 1.upto(HEIGHT) do |y| |
30 | 1.upto(WIDTH) do |x| |
31 | |
32 | # Calculate projection as a fraction of DIAGONAL
|
33 | dist_fxn = dist_from_origin(x, y).to_f / DIAGONAL |
34 | |
35 | lum = LUMINESCENCE_START + (LUMINESCENCE_END - LUMINESCENCE_START) * dist_fxn |
36 | |
37 | image[x - 1, y - 1] = ChunkyPNG::Color.from_hsl(HUE, 1, lum) |
38 | end
|
39 | end
|
40 | |
41 | image.save("background5.png") |

Lemon squeezy
So there you have it. We’ve not only generated a random-colour background, we’ve applied two different gradients to those colours. And I guess I can get back to doing all the things I was supposed to be doing before this distraction came along.
-
Previously I’d been using Unsplash’s app for OS X to select a random image from their site, but I was wondering if having busy backgrounds actively breaks me out of focus during the day. The obvious solution was to build a series of solid-colour wallpapers - solid colour so there was nothing distracting, and a series so I didn’t have the same colour all the time. ↩
