Proc-gen crosswords from scratch
- Published
- 2021-09-20
- Tagged
I like crosswords. After doing enough of them, however, I decided to try to make my own. And given I want to make my own, why not ridiculously over-engineer the whole process with a procedural generation mechanism in ruby?
This is currently a work in progress, but this blog post will at least show you through the start of the crossword building process as it exists right now, and may allow me to springboard off of it onto more complex posts in the future.
What sort of crosswords?
Chances are you never thought about the different types of crossword. But there’s a few different types out there, and they look quite different!
, [Rex Parker](https://rexwordpuzzle.blogspot.com/2015/03/actor-david-of-dark-shadows-thu-3-19-15.html), and [Wikipedia](https://en.wikipedia.org/wiki/Crossword)](guardian_crossword.png)
, [Rex Parker](https://rexwordpuzzle.blogspot.com/2015/03/actor-david-of-dark-shadows-thu-3-19-15.html), and [Wikipedia](https://en.wikipedia.org/wiki/Crossword)](nyt_crossword.jpg)
, [Rex Parker](https://rexwordpuzzle.blogspot.com/2015/03/actor-david-of-dark-shadows-thu-3-19-15.html), and [Wikipedia](https://en.wikipedia.org/wiki/Crossword)](swedish_crossword.jpg)
From left to right: British/Australian, American, and Swedish/German style crosswords. Images from The Guardian, Rex Parker, and Wikipedia
Because I live in New Zealand, whose cultural heritage (at least in terms of crosswords) is British, we have a very British form of crossword. This means:
- Generally a 15 x 15 grid.
- Parallel clues can never be directly alongside one another (always at least one row of ‘blocks’ or coloured-in squares between parallel clues)
- 180 degrees of rotational symmetry (so if you rotate the crossword 180 degrees, the pattern of blocks and lights is the same).
- All the lights (white squares) are contiguous1
- (Generally) the minimum length for any given clue is three letters
So how should we try to make them?
For what it’s worth, there’s actually a few steps involved in my process2:
- Layout. This is the step where you create the grid of blocks and lights that actually forms the crossword proper.
- Assigning letters. This is the bit where you put the letters into the grid to give the answers.
- Clueing. This is the bit where you look at the answers you’ve got, and make clues. Clueing can’t really be automated; also, it’s the really fun bit.
In this post, we’ll talk about the first two attempts I made for laying out a crossword automatically
Layout attempt 1: Random allocation
After getting a bit of a framework together to represent a crossword in ruby, I figured I’d give it a first go.
My first crossword-creation process went something like this:
- Start with a grid which is made completely of blocks (i.e. dark cells).
- Add a certain random number of lights (white cells) until we hit a good ratio. Ensure when we add these, we always add the same block rotated 180 degrees to maintain symmetry.
- Examine the crossword to see if it’s ‘valid’ using the criteria above.
- If not, try again.
Unfortunately it’s not that easy to make valid crosswords using this method. You could run this algorithm for a million iterations and get not one crossword that worked. So. Absolute brute force was out.
Layout attempt 2: Build off a basic grid.
So, rebuffed by the idea of just randomly throwing blocks at a grid, I took a step back and did some reading. Almost immediately I found a pattern that was so obvious I didn’t immediately spot it: most crosswords start with a grid of blocks.3
So now we have a better procedure:
- Start with a pattern of blocks on a 15 x 15 grid. Each block should be two cells away from its neighbouring blocks.
- Step-by-step: a. Add a block to the grid b. Add the same block, rotated by 180 degrees, to maintain symmetry c. Check to see if the crossword is valid (and if not, undo this step)
- Continue step two until we’ve added a certain number of blocks or reach critical density.
Now it turns out that this works!
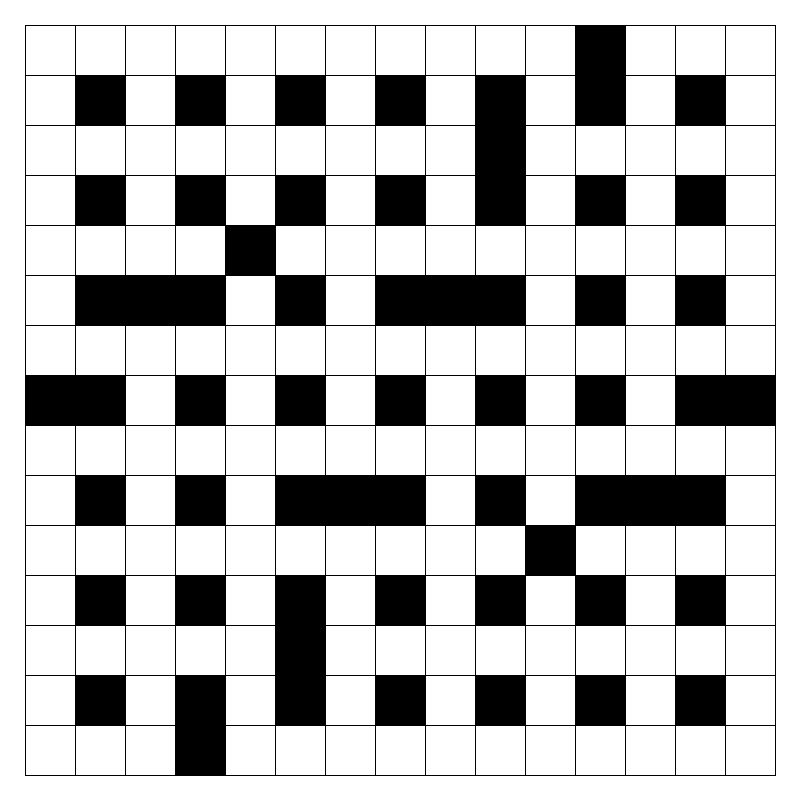
A surprisingly civilised crossword from a pretty basic algorithm.
Building on our basic algorithm
There’s a couple of issues this procedure will hit relatively quickly, however:
- Not every crossword will be as aesthetically pleasing as the one we built above.
- If we start increasing the number of blocks to add, we’re quickly going to enter the territory of crosswords with a gazillion length-three clues and several length-fifteen clues, rather than a pleasing selection of six- and eight-letter clues like we’d light.
- There’s no way for us to control the distribution of clue lengths!
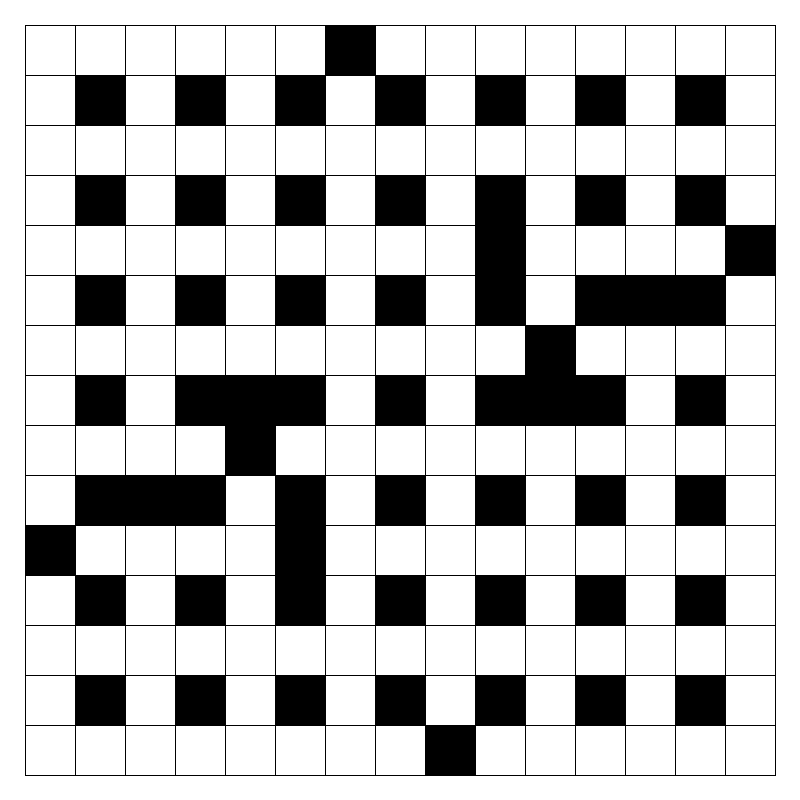
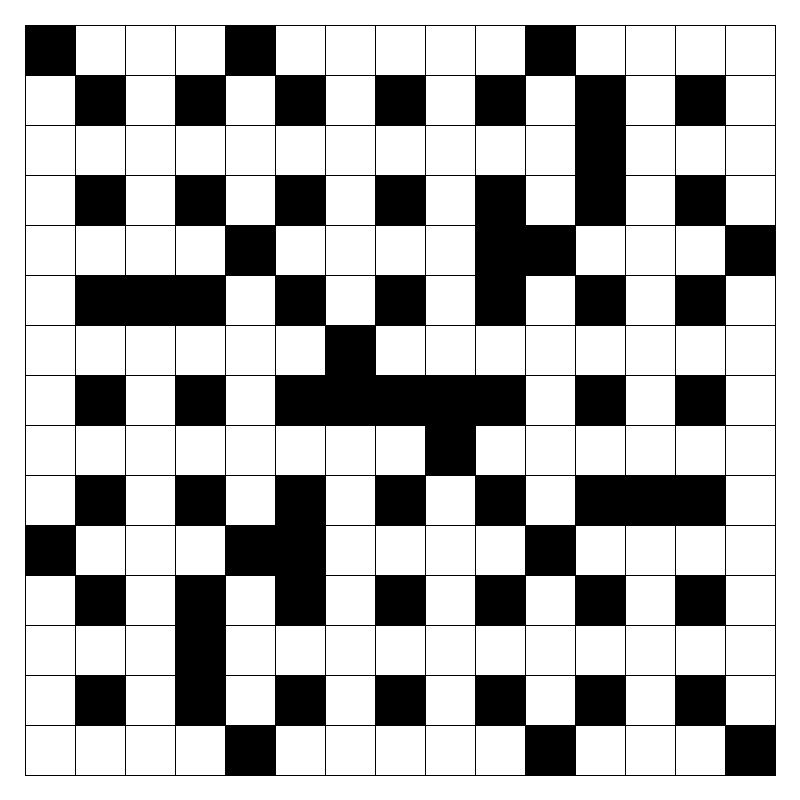
Some less pleasing crosswords. On the left a crossword with plenty more blocks and a bit less space; on the right, a crossword with a disturbing number of 15-long clues.
In order to make our crosswords more pleasing, we must first quantify what makes them less pleasing. And that means a little bit of statistical analysis.
Let’s look at the clue length distributions for the two crosswords featured above:
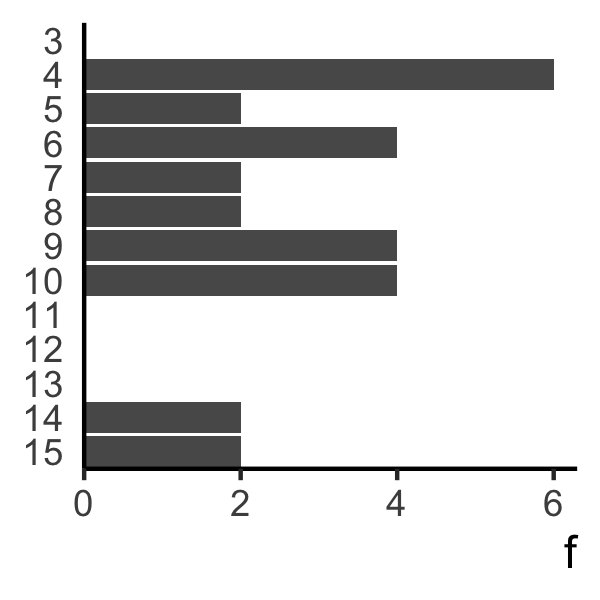
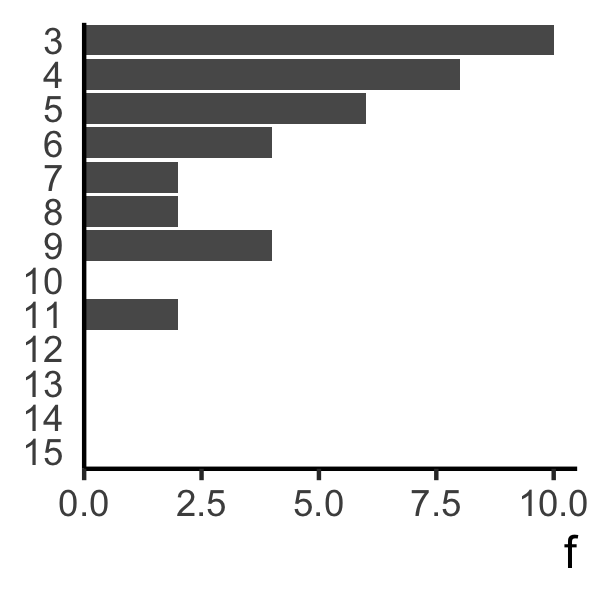
You can immediately see that our example on the left has four big chunky 14- and 15-character clues, which will make it if not impossible, at least challenging to fill in. Our example on the right, however, has a panoply of three-character clues, with a backing cast of four- and five-characters. Fine if you have plenty of them, I guess, but not great if you want to put some phrases or real head-scratchers into the grid.
So how can we control for clue size? One way is to change how many blocks we add. To create the crossword on the left, we started with a regular grid and added 5 blocks (and their rotational pairs). To create the crossword on the right, we added 10. In general, the more blocks you add, the shorter your clues get - that’s just how this works.
However, one way we can control for certain properties in this algorithm is to calculate a “score” for each crossword, depending on whether it fits our criteria for goodness. Let’s say we don’t want to have any more than two three-character-long clues in a given crossword, and we want the mean clue length to be around six (these are very specific examples, I know). Then we could calculate a ‘score’ for each crossword equal to:
1 | ABS([Average clue length] - 6) + MAX([Number of length 3 clues] - 2, 0) |
In this case, a lower score is better. If our crossword’s average clue length is exactly 6, and it has two or fewer 3-character-long clues, its score is zero! Chances are, though, its score will be higher.
Then, when we assign our blocks in the layout step, we could do something like the following:
- Identify five candidate positions where we could place our blocks. These should all be valid placements.
- Of these five candidates, calculate the ‘score’ for the resulting crossword in each case.
- Pick the lowest-scoring crossword.
And repeat until we’ve added enough blocks.
I’ve picked five candidates here, but that’s really a number I plucked out of the air. Three candidates might be a better number, or six. The more candidates we pick, the closer our crossword will match our criteria, but (I suspect) the less variation we’ll get in our overall layout.
Here’s a crossword I ginned up using these criteria:
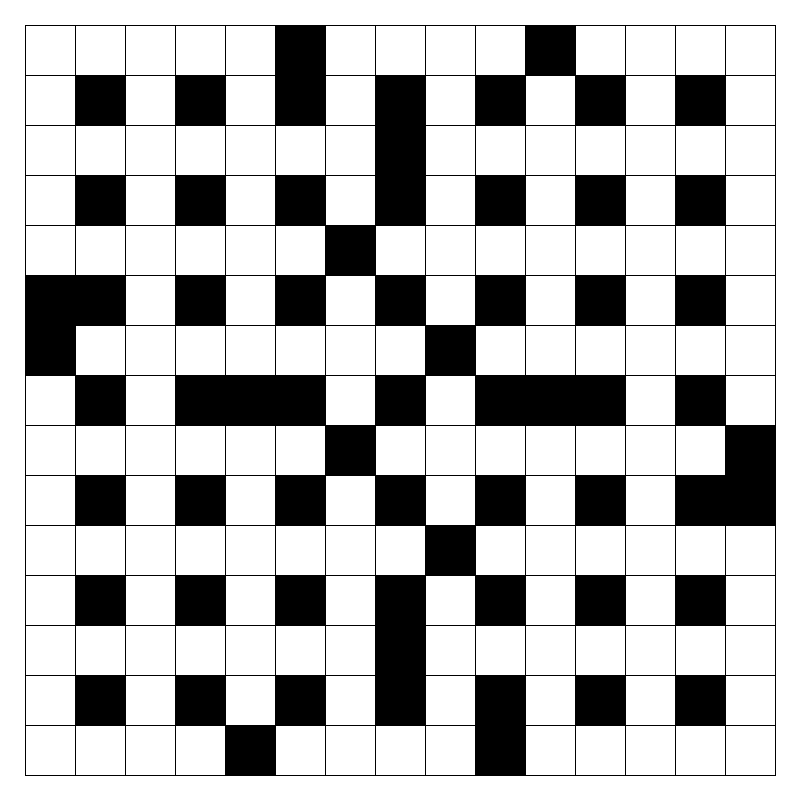
Not too shabby really
And here’s its clue length distribution plot:
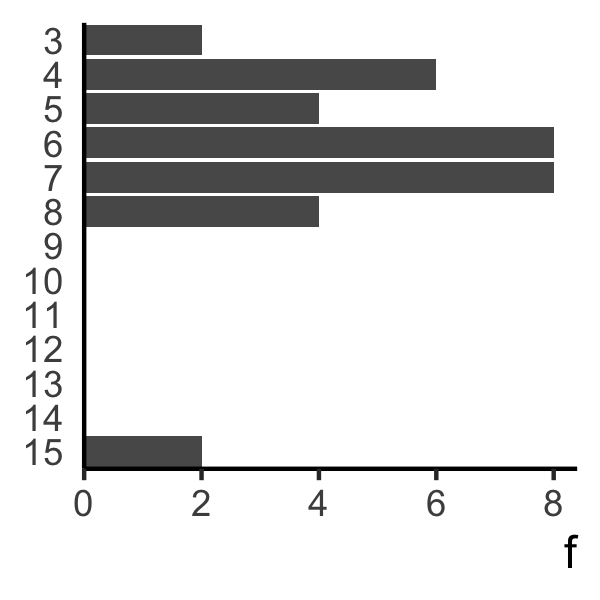
Its average clue length is 6.3, and as we can see, it has exactly two three-character-long clues. So our scoring mechanism works!
So what next?
At this stage we have a surprisingly robust random crossword layout algorithm. The next step, though, is to add clues. We’ll see if that ever lands on here.
-
If you’re reading this list and going “Well yeah, doesn’t that apply to every crossword?”, you should check out the Wikipedia page on crosswords some time! ↩
-
I’m going about this on my own, without really engaging with any form of crossword setting community. That means that these terms may be way out of line with terms other people use for these steps. That’s learning! ↩
-
This article, and the articles on Crossword Unclued, have enough good information in them that we’ll probably be returning to them soon. ↩
