I’ve previously discussed Gnuplot on this blog, discussing why it’s excellent and demonstrating how to make a semi-decent simple graph using the package. You can learn a lot from Gnuplot by playing with sample graphs and reading the documentation, but I thought I could show off some of the more complex graphs I’ve made over the past year or so, and how I went about crafting them.
The setup
In this post I’ll cover a somewhat complex particle sizing graph I ended up producing for a recent paper1. In the paper we were determining the size of a batch of elliptical nanoparticles, which we could image using scanning electron microscopy (SEM). SEM produces an image of the material at high resolution, in greyscale:

While the image looks very nice, right now it’s just that: an image. It’s tricky to compare images against each other, especially when we’re interested in things like average particle size and what-have-you. So what we want to do is measure the size of these particles and then graph particle size across different samples.
Because these particles are elliptical, we can measure their size by measuring their major and minor diameters: that is, the thickness of the particle where it’s thickest and where it’s thinnest.
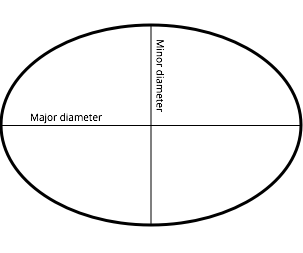
If you measure enough of these, you get an idea of the overall particles’ size and anisotropy (i.e. ratio between the two diameters). However, this takes a long time, and you can never be sure that the area you’re measuring is representative of the sample as a whole. Techniques like dynamic light scattering are much faster, but only get you an average radius (i.e. they assume the particles are spherical) as well as standard deviation. There’s also no guarantee that you’re measuring the individual particle and not clumps of them drifting around in solution together. The best way to get an idea of average particle size, is to use two techniques like this together and see how the data compares.
In our paper we ended up comparing both SEM and DLS data (which means we get a good idea of anisotropy and particle shape from the SEM, but a check that our results are representative from the DLS). The problem is then how to graph SEM data (especially if we want to graph major and minor diameters) and DLS data on the same graph. If we had just one series (just the DLS data, for example) we could do a nice scatter-graph, but with major and minor diameters by SEM particle sizing and average particle diameter by DLS, plus variance in each point, you’re looking at a lot of data per sample. Add in several samples, and the scatter-plot graph quickly gets unmanageable:
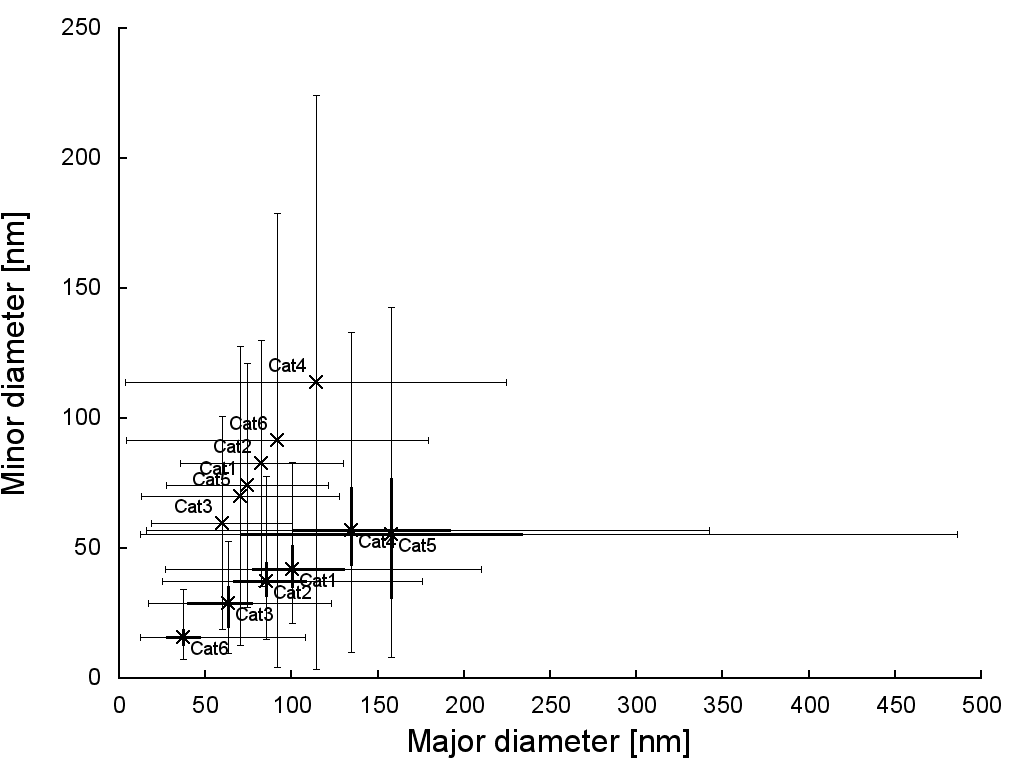
…and this means what, exactly?
The problem here is that we have a lot of data to graph: an average size, maximum, and minimum value for SEM and DLS. The SEM data can be further subdivided because we have major and minor diameter values.
The one thing that unites all this data is that we’re able to group it by sample. Since all of the data has this variable in common, I thought I could do something more like your standard bar graph. In fact, given all the data is ranges, I realised I could go back to a graph I hadn’t touched since Year 12 maths: the box-and-whisker plot.
The graph
Once I’d worked my way through how to visualise the data, my plan clicked into place. Each sample would be represented on the y-axis of my graph,2 with different sets of data represented by different lines:
There’s three sets of data I need to graph for each sample:
- SEM minor diameter
- DLS average diameter
- SEM major diameter
Assuming everything goes to plan, the DLS average diameter should fall between the minor and major diameter. In addition, since we have a bit more data from our SEM plots and can box-and-whisker them, these graphs will look slightly different from the DLS plots. This is what our final graph should look like:
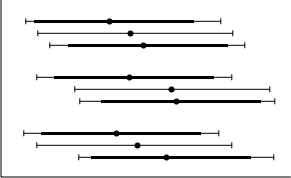
The new-look graph, with box-and-whisker, order, and mean value dots.
It’s quite a complex-looking graph, and while it’s no plain sailing, it’s still doable in Gnuplot. Let’s see how it’s done.
Step 1: Plotting the DLS
Data analysis was performed in Microsoft Excel, boon of casual analysts everywhere, and the sort of formulae I used to get nice values out of that could be the subject a whole different post. For the meantime, let’s assume that everything can be copied out nicely.
The DLS data is pretty simple: each category simply needs a mean value and a range (which determines the position of the bars’ start and end). We ended up sizing six samples, which I’ve marked “Cat1” through “Cat6” in the following data sets:
1 | # dls.dat |
2 | ID Mean Range |
3 | Cat1 74.33598071 46.83827692 |
4 | Cat2 82.62131831 47.34548776 |
5 | Cat3 59.69341385 40.89532088 |
6 | Cat4 113.97944 110.4312038 |
7 | Cat5 70.16979667 57.3582166 |
8 | Cat6 91.6090325 87.3517587 |
We can plot this data purely by using the xerrorbars plotting style. A sample graph might look like this:
1 | set terminal png size 1024,768 font "Arial,18pt" |
2 | set output "graph-dls.png" |
3 | set border 3 lw 2 |
4 | unset key |
5 | |
6 | set tics nomirror |
7 | unset ytics |
8 | set yrange [5.5:-0.5] |
9 | set lmargin 6 |
10 | |
11 | set xlabel "Particle diameter [nm]" font "Arial,24pt" |
12 | set xrange [0:] |
13 | |
14 | set style line 1 lc rgb "black" ps 1 pt 7 # For DLS |
15 | |
16 | plot\ |
17 | "dls.dat" using (column("Mean")):0:(column("Range")) with xerrorbars ls 1,\
|
18 | "dls.dat" using (0):0:(column("ID")) with labels right offset -1,0
|
There’s a lot to go through here, so let’s take it a group at a time.
The first paragraph in the above code (lines 1–4) sets our image type, size and default colour. We then specify the name of the file to write to, and set up the type of border (including giving it a sexy thick line-width) and removing the key, which we don’t need. This is all basic setup stuff that I either do by default now or import from a text snippet.
The next paragraph deals with axes and tics. set tics nomirror removes the ugly mirroring of tics on opposite axes - I’m not sure why this is default, but it is. We then remove default tics on the y-axis (which we’ll replace ourselves later), set the range so it plays nice with our categories3, and finally give ourselves a bit of space on the left margin to play around with. The x-axis gets a label, and we ensure it starts at 0 like a well-behaved graph.
We plot two series: our DLS data and some y-axis labels. The DLS data uses xerrorbars, which takes x, y, and xdelta values. The shape, size and colour of the points is set up by our previously-defined line style. I’m using the optional column syntax for columns here as it makes everything easier to parse. The one trick here is the column 0, which is simply equal to the line number of the particular entry. This arrays our data down the page nicely.
(Side note: Astute readers will note that if line 1 is graphed at y = 1, line 2 is graphed at y = 2, etc., our data should travel up the page, not down. I handily stopped this happening by reversing my yrange, as defined on line 8.)
The labels (line 18) use column 0 again, but also (0). There’s a key difference here - anything outside of a set of parentheses in a using block is considered to refer to a column number, while anything inside parentheses is evaluated as a number or function. Thus, 0 means “column 0”, but (0) means “the number 0”. This arrays our labels nicely against the y-axis, and the right alignment and offset place them just to the left of the axis proper.
All of this combines to give us the following graph:
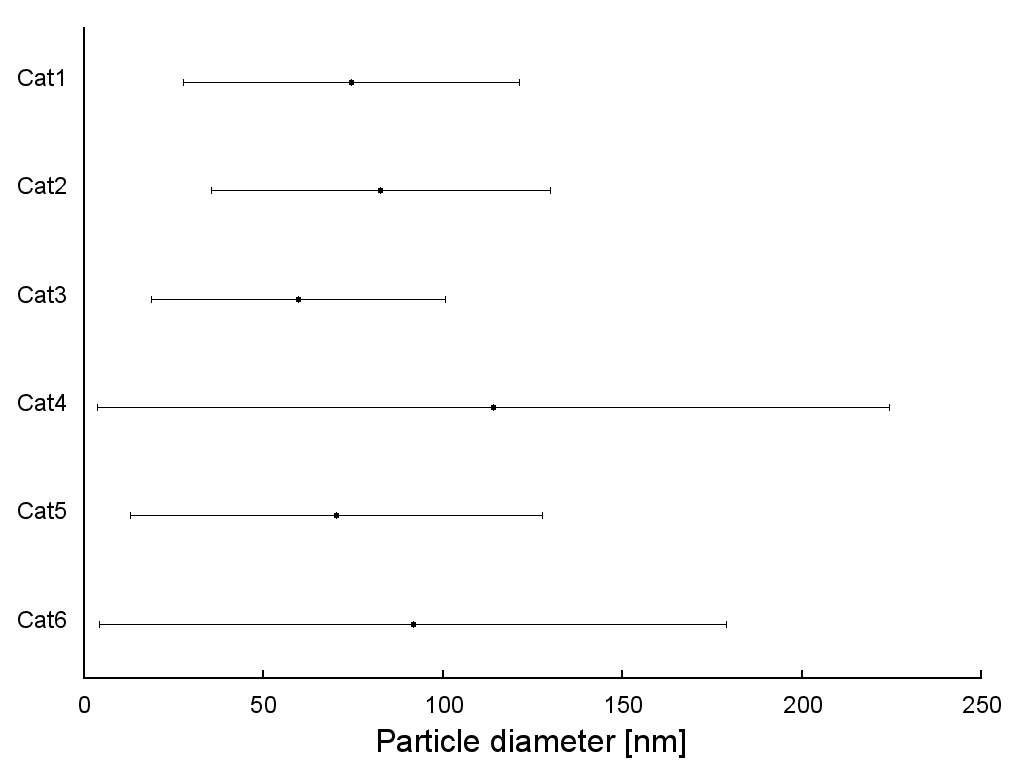
Step 2: Plotting the SEM data
This is where the graph gets complex. We have a lot of SEM data, and I take advantage of Gnuplot’s index function to keep it nicely maintained in one file. Each SEM plot is actually made up of three different plots: one for the range, one for the quartiles, and one for the median:

A breakdown of the SEM graph
I’m keeping the data organised in the file like this:
1 | # sem.dat |
2 | #Major |
3 | ID Min Lower Median Upper Max |
4 | Cat1 26.656 77.6935 100.311 129.947 210.112 |
5 | Cat2 24.903 66.545 85.28 107.744 175.556 |
6 | Cat3 17.028 40.23925 63.3445 76.32425 122.745 |
7 | Cat4 15.923 100.83 134.538 191.205 342.209 |
8 | Cat5 12.305 70.712 157.572 232.9205 485.904 |
9 | Cat6 12.111 27.70375 37.349 46.213 108.076 |
10 | |
11 | |
12 | #Minor |
13 | ID Min Lower Median Upper Max |
14 | Cat1 21.105 35.474 42.0965 50.59825 83.022 |
15 | Cat2 14.875 31.893 37.457 44.202 77.509 |
16 | Cat3 9.458 19.97425 28.9185 35.18075 52.711 |
17 | Cat4 10.041 44.008 56.901 72.964 133.113 |
18 | Cat5 8.205 31.103 55.534 76.555 142.678 |
19 | Cat6 7.438 13.084 15.7415 18.62075 34.139 |
Let’s plot our SEM minor diameter slightly above the DLS bar: in this case our y-value will be ($0-0.2) (i.e. row number subtract 0.2).
Our quartile range can be represented by a thick line. Gnuplot’s vector plot style handily does the job for us: we can make it nice and thick with a custom line style. Because the values for vector plots are x:y:xdelta:ydelta, we need to do a bit of math to plot these correctly:
1 | set style line 2 lc rgb "black" lw 3 #Used for quartiles |
2 | plot "sem.dat" index "Minor" using (column("Lower")):($0-0.2):(column("Upper")-column("Lower")):(0) with vectors ls 2 nohead
|
The nohead declaration removes the arrow-head from these lines.
We also need to plot the range and median. Since we can’t guarantee that the median will fall right in the middle, we have to do a bit of jiggery-pokery with the data to place our x error-bars correctly:
1 | plot "sem.dat" index "Minor" using (column("Median")):($0-0.2):(column("Min")):(column("Max")) with xerrorbars ls 1
|
We do a very similar thing for the SEM major diameter, which gives us the following package of plotting and line styles:
1 | set style line 1 lc rgb "black" ps 1 pt 7 # For DLS/SEM median |
2 | set style line 2 lc rgb "black" lw 3 # For quartiles |
3 | |
4 | plot\ |
5 | "dls.dat" using (column("Mean")):0:(column("Range")) with xerrorbars ls 1,\
|
6 | "dls.dat" using (0):0:(column("ID")) with labels right offset -1,0,\
|
7 | "sem.dat" index "Minor" using (column("Median")):($0-0.2):(column("Min")):(column("Max")) with xerrorbars ls 1,\
|
8 | "sem.dat" index "Major" using (column("Median")):($0+0.2):(column("Min")):(column("Max")) with xerrorbars ls 1,\
|
9 | "sem.dat" index "Minor" using (column("Lower")):($0-0.2):(column("Upper")-column("Lower")):(0) with vectors ls 2 nohead,\
|
10 | "sem.dat" index "Major" using (column("Lower")):($0+0.2):(column("Upper")-column("Lower")):(0) with vectors ls 2 nohead
|
Once you stick the original header on top, you get something very nice indeed:
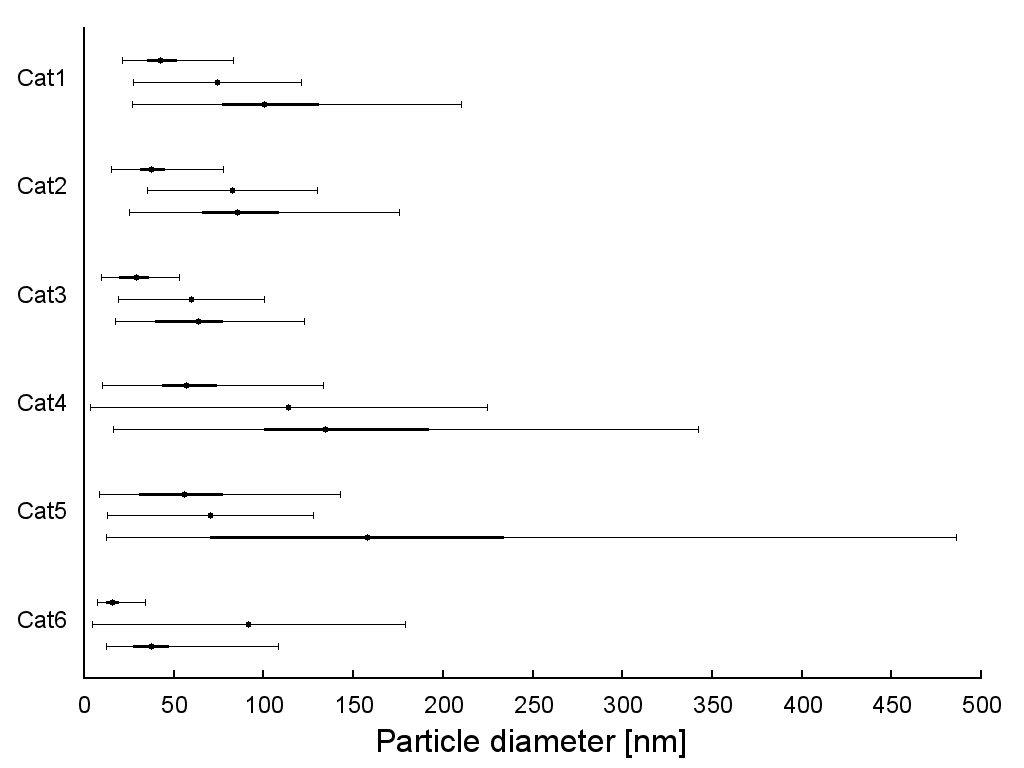
The finished product
So there we have it. Complex data plotted. Like many systems, Gnuplot is only intimidating at first. The steep learning curve levels off pretty abruptly, and you’ll soon be producing clean-looking, technically-complex graphs with ease.
-
Now in print with RSC Advances ↩
-
If I’m graphing data in one dimension (as I’m doing here) I tend to prefer putting that value on the x axis of the graph, with my bars or what-have-you stretching left to right. It also gives me plenty of space to label the bars, without having to rotate text. ↩
-
Note that the range starts at 5.5 and finishes at -0.5. I’ve reversed it, and this will be important later. ↩
